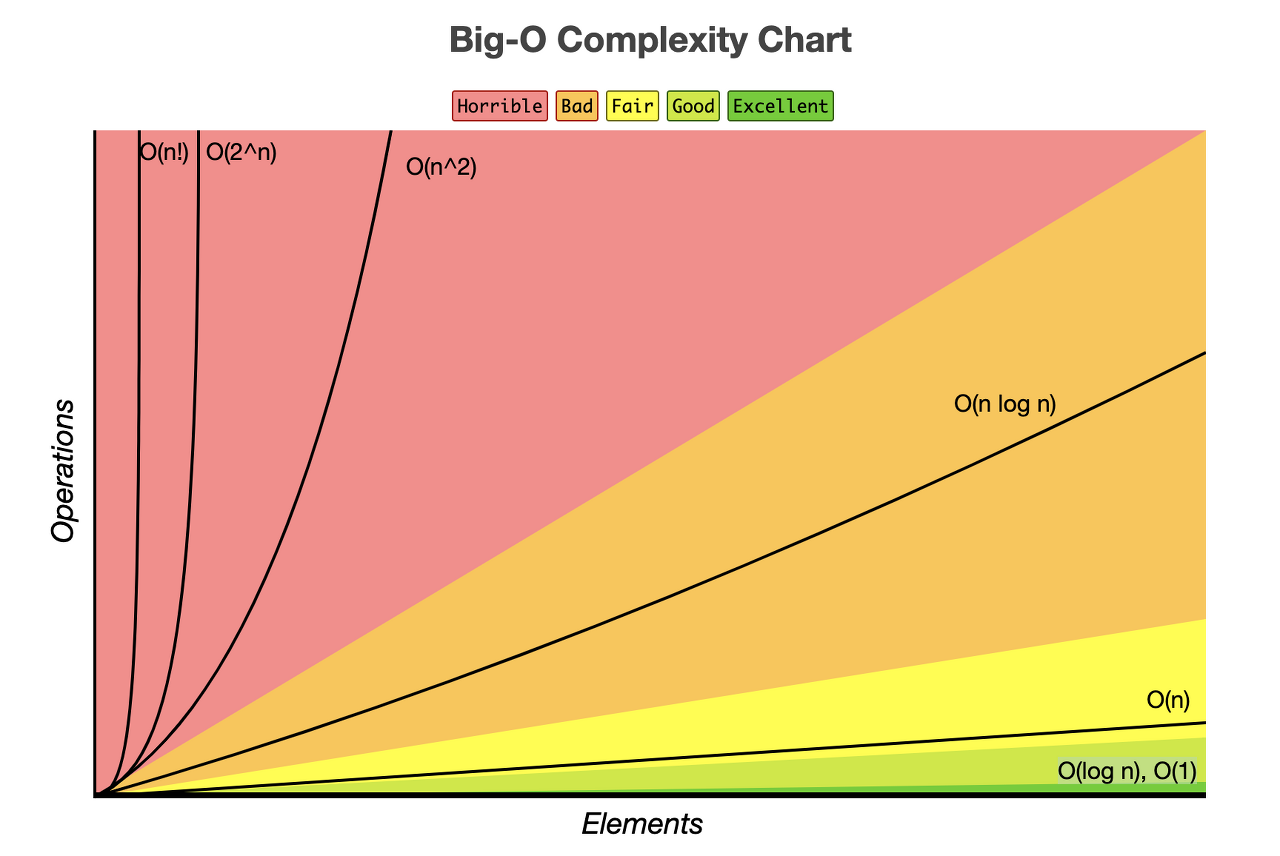
시간 복잡도
위에 그래프의 모습에서 보이는 것처럼 간단한 출력과 같은 O(1) 혹은 단순한 증가함수인 O(n), O(log n ) 들과
O(n^2), O(2^n)의 그래프의 기울기가 큰 차이가 나타나는 걸 볼 수 있습니다.
컴퓨터가 계산할 때 사용하는 알고리즘,함수에 따라 값에 증가에 따른 결괏값을 구하는 시간이 달라지는데
이를 시간 복잡도라고 얘기합니다.
시간 복잡도를 고려해야 하는 이유
우리가 프로그램을 만들 때 구현하려는 값을 어떤 알고리즘을 이용해 구현하느냐에 따라 그 프로그램의 최적화에 영향이 가기에 항상 어떻게 하면 더 효율적으로 구현할 수 있는지 고민해야 하며
알고리즘 문제를 풀 때도 문제에서 원하는 시간을 초과하면 문제를 풀 수 없는 경우도 있기에
어떠한 방식으로 알고리즘을 구현할지 생각할 때 시간복잡도는 필수적으로 생각해야하는 조건입니다.
표기법 종류
위 그래프에서 보이는 것처럼 시간복잡도의 효율성에 따라서 구분되는 알고리즘에 따른 표기법이 있습니다.
효율성 : O(1) >O(log n) > O(n) > O(n x log n) > O(n^2) > O(2^n)
대표 알고리즘
- : Operation push and pop on Stack
- g n): Binary Tree
- ): for loop
- ×log n): Quick Sort, Merge Sort, Heap Sort
- 2): Double for loop, Insert Sort, Bubble Sort, Selection Sort
- n): Fibonacci Sequence
1. O(1)
O(1)은 입력값이 증가하더라도 시간이 늘어나지 않는 , 상수입니다.
public class TimeComplexity {
public static void main(String[] args) {
int[] ints = {1,2,3,4};
O1 o1 = new O1();
int num = o1.play(ints,2);
System.out.println(num); //출력 : 3
}
}
class O1{
int play(int[] nums,int index){
return nums[index];
}
}
원하는 index의 값을 넣어 바로 값을 구할 수 있습니다. 입력값이 증가하더라도 구하는 시간은 증가하지 않을 때
O(1)이라고 표기를 합니다.
2. O(log n)
단순 순환(O(n)) 이 아닌 1/2 씩 경우의 수를 줄여 나가며 탐색하는 알고리즘을 이용할 때 사용하는 표기법입니다.
BST(Binary Search Tree) 의 경우가 여기에 해당합니다.
class Tree {
int count = 0;
class Node {
int data;
Node left;
Node right;
Node (int data) {
this.data = data;
}
}
Node root;
public void makeTree(int[] a) {
root = makeTreeR(a, 0, a.length -1);
}
public Node makeTreeR(int[] a, int start, int end) {
if (start > end) return null;
int mid = (start + end) /2;
Node node = new Node(a[mid]);
node.left = makeTreeR(a, start, mid - 1);
node.right = makeTreeR(a, mid+1,end);
return node;
}
public void searchBTree (Node n, int find) {
if (find <n.data) {
System.out.println("Data is smaller than " + n.data);
searchBTree(n.left, find);
}else if (find >n.data) {
System.out.println("Data is bigger than " + n.data );
searchBTree(n.right, find);
}else {
System.out.println("Data found!");
}
count++;
System.out.println("반복횟수는 " +count + " 입니다");
}
}
public class Test {
public static void main(String[] args) {
int[] a = {1,2,3,4,5,6,7,8,9,10};
Tree t = new Tree();
t.makeTree(a);
t.searchBTree(t.root,1);
}
}
//출력
Data is smaller than 5
Data is smaller than 2
Data found!
반복횟수는 1 입니다
반복횟수는 2 입니다
반복횟수는 3 입니다
이 코드는 BST를 구현한 코드입니다.
코드를 보면 전체 배열의 가운데에 위치한 값을 기준으로 왼쪽에 본인보다 작은 수, 오른쪽에 본인보다 큰 수로 나누어
그걸 반복하여 Tree 를 만들고 그 트리를 순환하여 값을 찾아냅니다.
즉, 계속 1/2을 통해 경우의 수를 반으로 줄인 뒤에 탐색을 하는 과정을 반복합니다.
이러한 매커니즘 덕분에 일반적인 반복문을 통해(O(n)) 값을 찾는 것보다 훨씬 효율적으로 찾아낼 수 있습니다.
3. O(n)
입력값이 증가함에 따라 같은 비율로 증가함을 의미합니다.
주로 반복문을 통한 값을 찾을 때 O(n)의 시간복잡도를 가집니다.
public class TimeComplexity {
public static void main(String[] args) {
int[] ints = {1,2,3,4};
O1 o1 = new O1();
int num = o1.play(ints,2);
System.out.println(num); //출력 1 (숫자 2의 index값)
}
}
class O1{
int num;
int play(int[] nums,int n){
for(int i=0; i<nums.length; i++){
if(nums[i]==n){
num=i;
}
}
return num;
}
}
간단한 반복문을 통해 n의 index값을 찾는 코드입니다.
4. O(n^2)
입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가함을 의미합니다.
주로 2중 반복문을 사용할 때 O(n^2)의 시간복잡도를 가집니다.
3중,4중,5중으로 반복문을 사용해도 같이 O(n^2)라고 표기합니다.
public class TimeComplexity {
public static void main(String[] args) {
int[] ints = {1,2,2,4,5,10,2};
O1 o1 = new O1();
int num = o1.play(ints);
System.out.println(num); //출력 3 (ints 배열에서 중복된 숫자의 개수)
}
}
class O1{
int count=0;
int maxNum=0;
int play(int[] nums){
for(int i=0; i<nums.length; i++){
for(int j=0; j<nums.length; j++){
if(nums[i]==nums[j]){
count++;
if(maxNum<count) {
maxNum = count;
}
}
}
count=0;
}
return maxNum;
}
}
2중 반복문을 통해 ints 배열 안에 중복된 숫자 중 가장 많이 중복된 숫자의 개수를 구하는 코드
5. O(2^n)
n번 반복할 수록 2의 n제곱만큼 시간이 증가함을 의미합니다.
n의 값이 10일 때 처리 시간이 10초가 걸렸다면 n의 값이 20일 경우 처리 시간이 10x 2^10초 필요하게 됨을 의미합니다.
주로 재귀로 구현하는 피보나치 수열이 O(2^n)의 시간 복잡도를 가집니다.
public class TimeComplexity {
public static void main(String[] args) {
O5 o5 = new O5();
Print print = new Print();
int num = o5.play(10);
System.out.println(num); // 55
System.out.println(print.printFibo(10)); // [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
}
}
class O5{
int play(int n){
if(n==0) return 0;
if(n==1) return 1;
return play(n-1) + play(n-2);
}
}
class Print extends O5{
List<Integer> list = new ArrayList<>();
List<Integer> printFibo(int n){
for(int i=0; i<=n; i++ ){
list.add(play(i));
}
return list;
}
}
//출력
55
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]
재귀를 통해 피보나치 수열의 원하는 자릿수의 값을 구하고, 반복문을 통해 피보나치수열로 구성된 List를 구현한 코드입니다. 재귀를 통해 구현하여 굉장히 코드가 간결해져 직관적으로 봤을 때는 효율적으로 보이지만 실제로는 시간 복잡도가 굉장히 심해 상당히 비효율적인 방법입니다.
따라서 재귀함수를 사용하지 않아도 시간복잡도가 낮은 다른 알고리즘을 통해 구현할 수 있다면
효율성을 위해 다른 알고리즘을 구현할 수 있어야 합니다.
그렇다면 방금 위에서 구한 피보나치 수열을 O(n^2) 방식이 아닌 다른 방식으로 어떻게 구할 수 있을까요?
효율적으로 구현한 피보나치 수열
public class TimeComplexity {
public static void main(String[] args) {
O5 o5 = new O5();
int num = o5.fibo(10);
System.out.println(num); //출력 55
}
}
class O5{
int x = 0;
int y = 1;
int sumNum =0;
int fibo(int num) {
if(num==0) return 0;
if(num==1) return 1;
for(int i=0; i<=num-2; i++) {
sumNum = x + y;
x = y;
y = sumNum;
}
return sumNum ;
}
}
위 코드처럼 피보나치 수열의피보나치수열의 원리를 이용해서 간단한 방식으로 피보나치수열의 값을 구할 수 있습니다.
기존의 피보나치 수열은 O(2^n)의 시간 복잡도를 가져서 시간의 효율성이 굉장히 떨어지는 반면
위 코드는 for문을 이용해서 구했기 때문에 시간복잡도가 O(n) 이 되어 효율성이 굉장히 좋아졌다는 걸 알 수 있습니다.
마무리
시간복잡도의 여러 종류에 따른 표기 및 그 표기들이 각각 어떤 의미를 가지고 어떤 알고리즘에서 주로 사용되는지 예시 코드를 통해 확인해 보았습니다.
큰 시점으로 봤을 때 시간 복잡도는 프로그래밍을 할 때 프로그램 자체의 효율성을 위해서 개발자가 항상 생각해야 할 개념이기에 모든 코드를 구현할 때 어떻게 하면 더 효율적이게 , 시간복잡도가 낮은 코드로 구현할 수 있을까란 생각을 가지고 접근해야 하며
작은 시점으로 봤을 때 코딩 테스트를 위해 각 시간 복잡도에 따른 대표적인 문제들을 숙지하고, 이해할 수 있어야 하며
시간 복잡도가 높은 알고리즘을 더 효율성 높게 만들 수 있는 케이스는 특히 더 공부하여 숙달해야 된다고 생각합니다.
코딩 테스트 문제를 풀기 위해 접근법을 생각할 때, 아이디어를 떠올리기 이전 '어떤 시간복잡도를 이용하여 풀 수 있을까?'라는 전제조건으로 접근해야 하며 특히 시간 효율성을 중요시 여기는 문제인 경우에는 O(n) , O(log n) 등을 어떤 식으로 구현할 것인지 생각하며 접근하는 게 중요할 거라 여겨집니다.
'Algorithm' 카테고리의 다른 글
| Selection Sort - Sorting Elements by Selection -JAVA (0) | 2023.06.13 |
|---|---|
| 선택 정렬(Selection Sort) - 자바(JAVA) (0) | 2023.06.13 |
| 우선순위 큐(Priority Queue) - 자바(JAVA) (0) | 2023.06.13 |
| DP(Dynamic Programming) - 자바(JAVA) (0) | 2023.06.13 |
| [백준] 1676번 팩토리얼 0의 개수 (실버5) (0) | 2023.02.20 |